Credit Risk Modeling (details + scripts)
Data:
I use the German credit data set. The data is provided in two formats, one consists of 20 variables (7 numerical, 13 categorical) as below:
– Status of existing checking account
– Duration in month (numerical)
– Credit history
– Purpose
– Credit amount (numerical)
– Savings account/bonds
– Present employment since
– Installment rate in percentage of disposable income (numerical)
– Personal status and sex
– Other debtors / guarantors
– Present residence since (numerical)
– Property
– Age in years (numerical)
– Other installment plans
– Housing
– Number of existing credits at this bank (numerical)
– Job
– Number of people being liable to provide maintenance for (numerical)
– Telephone
– foreign worker
and the other one contains 24 numerical variables for algorithms which strictly works with numerical variables. In the both formats the default, target variable shows whether the loan applicant could make payment (0/NonDef) or not (1/Def).
After loading data sets as the data frames I check the distribution of variables and possibility of missing data. Fortunately there is no any abnormal behavior and missing data in both data sets. The summary of both formats of data sets are as following:
R> d.g <- read.table('./data/german.data')
R> colnames(d.g) <- c( 'account_balance',
'months_loan_duration',
'credit_history',
'purpose',
'credit_amount',
'savings_balance',
'employment_status',
'installment_rate',
'personal_status',
'other_debtors_guarantors',
'present_residence_years',
'property',
'age',
'other_installment',
'housing',
'number_credits_this_bank',
'job',
'number_dependents',
'phone',
'foreign_worker',
'default')
R> d.g$default <- factor(ifelse(d.g$default==1, 0, 1))
R> levels(d.g$default) <- c('Nondef', 'Def')
R> summary(d.g)
account_balance months_loan_duration credit_history purpose
A11:274 Min. : 4.0 A30: 40 A43 :280
A12:269 1st Qu.:12.0 A31: 49 A40 :234
A13: 63 Median :18.0 A32:530 A42 :181
A14:394 Mean :20.9 A33: 88 A41 :103
3rd Qu.:24.0 A34:293 A49 : 97
Max. :72.0 A46 : 50
(Other): 55
credit_amount savings_balance employment_status installment_rate
Min. : 250 A61:603 A71: 62 Min. :1.000
1st Qu.: 1366 A62:103 A72:172 1st Qu.:2.000
Median : 2320 A63: 63 A73:339 Median :3.000
Mean : 3271 A64: 48 A74:174 Mean :2.973
3rd Qu.: 3972 A65:183 A75:253 3rd Qu.:4.000
Max. :18424 Max. :4.000
personal_status other_debtors_guarantors present_residence_years property
A91: 50 A101:907 Min. :1.000 A121:282
A92:310 A102: 4 1 1st Qu.:2.000 A122:232
A93:548 A103: 52 Median :3.000 A123:332
A94: 92 Mean :2.845 A124:154
3rd Qu.:4.000
Max. :4.000
age other_installment housing number_credits_this_bank
Min. :19.00 A141:139 A151:179 Min. :1.000
1st Qu.:27.00 A142: 47 A152:713 1st Qu.:1.000
Median :33.00 A143:814 A153:108 Median :1.000
Mean :35.55 Mean :1.407
3rd Qu.:42.00 3rd Qu.:2.000
Max. :75.00 Max. :4.000
job number_dependents phone foreign_worker default
A171: 22 Min. :1.000 A191:596 A201:963 Nondef:700
A172:200 1st Qu.:1.000 A192:404 A202: 37 Def :300
A173:630 Median :1.000
A174:148 Mean :1.155
3rd Qu.:1.000
Max. :2.000
and the numerical format:
R> d.g.num <- read.table('../data/german.data-numeric')
R> d.g.num$default <- factor(ifelse(d.g.num$V25==1, 0, 1))
R> d.g.num$V25 <- NULL
R> summary(d.g.num)
V1 V2 V3 V4
Min. :1.000 Min. : 4.0 Min. :0.000 Min. : 2.00
1st Qu.:1.000 1st Qu.:12.0 1st Qu.:2.000 1st Qu.: 14.00
Median :2.000 Median :18.0 Median :2.000 Median : 23.00
Mean :2.577 Mean :20.9 Mean :2.545 Mean : 32.71
3rd Qu.:4.000 3rd Qu.:24.0 3rd Qu.:4.000 3rd Qu.: 40.00
Max. :4.000 Max. :72.0 Max. :4.000 Max. :184.00
V5 V6 V7 V8
Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
1st Qu.:1.000 1st Qu.:3.000 1st Qu.:2.000 1st Qu.:2.000
Median :1.000 Median :3.000 Median :3.000 Median :3.000
Mean :2.105 Mean :3.384 Mean :2.682 Mean :2.845
3rd Qu.:3.000 3rd Qu.:5.000 3rd Qu.:3.000 3rd Qu.:4.000
Max. :5.000 Max. :5.000 Max. :4.000 Max. :4.000
V9 V10 V11 V12
Min. :1.000 Min. :19.00 Min. :1.000 Min. :1.000
1st Qu.:1.000 1st Qu.:27.00 1st Qu.:3.000 1st Qu.:1.000
Median :2.000 Median :33.00 Median :3.000 Median :1.000
Mean :2.358 Mean :35.55 Mean :2.675 Mean :1.407
3rd Qu.:3.000 3rd Qu.:42.00 3rd Qu.:3.000 3rd Qu.:2.000
Max. :4.000 Max. :75.00 Max. :3.000 Max. :4.000
V13 V14 V15 V16
Min. :1.000 Min. :1.000 Min. :1.000 Min. :0.000
1st Qu.:1.000 1st Qu.:1.000 1st Qu.:1.000 1st Qu.:0.000
Median :1.000 Median :1.000 Median :1.000 Median :0.000
Mean :1.155 Mean :1.404 Mean :1.037 Mean :0.234
3rd Qu.:1.000 3rd Qu.:2.000 3rd Qu.:1.000 3rd Qu.:0.000
Max. :2.000 Max. :2.000 Max. :2.000 Max. :1.000
V17 V18 V19 V20
Min. :0.000 Min. :0.000 Min. :0.000 Min. :0.000
1st Qu.:0.000 1st Qu.:1.000 1st Qu.:0.000 1st Qu.:0.000
Median :0.000 Median :1.000 Median :0.000 Median :0.000
Mean :0.103 Mean :0.907 Mean :0.041 Mean :0.179
3rd Qu.:0.000 3rd Qu.:1.000 3rd Qu.:0.000 3rd Qu.:0.000
Max. :1.000 Max. :1.000 Max. :1.000 Max. :1.000
V21 V22 V23 V24 default
Min. :0.000 Min. :0.000 Min. :0.0 Min. :0.00 0:700
1st Qu.:0.000 1st Qu.:0.000 1st Qu.:0.0 1st Qu.:0.00 1:300
Median :1.000 Median :0.000 Median :0.0 Median :1.00
Mean :0.713 Mean :0.022 Mean :0.2 Mean :0.63
3rd Qu.:1.000 3rd Qu.:0.000 3rd Qu.:0.0 3rd Qu.:1.00
Max. :1.000 Max. :1.000 Max. :1.0 Max. :1.00
Methodology
I will apply logistic regression, decision tree and random forest on these data sets and evaluate their efficiency based on AUC (Area Under ROC), Kappa statistics and Bad Rate. Finally I will propose the best model which shows the best efficiency on the training data set.
1- Logistic Regression
First I divide the data to the test and training data sets. For this purpose I employ createDataPartition function from caret package to obtain the stratified random samples of the data. I will use the training set for training the algorithm and finding the most efficient model and keep the test data set to check the real performance of the selected model on an unseen data set.
R> prop.table(table(d.g.num$default)) 0 1 0.7 0.3 R> library(caret) R> in_train <- createDataPartition(d.g.num$default, p = 0.66, list = FALSE) R> train_set <- d.g.num[in_train,] R> test_set <- d.g.num[-in_train,] R> prop.table(table(train_set$default)) 0 1 0.7 0.3 R> prop.table(table(test_set$default)) 0 1 0.7 0.3
I start by the most general model which includes all variables then construct the next model by omitting the predictor which has the worst p-value. Since the p-values of predictors have high dependency to training data set I calculate the average p-values through cross-validation in training data set. The pvalue.coef function return the p-values of coefficients of a given model.
R> pvalue.coef <- function(mdl)
+ {
+ dum <- summary(mdl)$coefficients
+ dum <- dum[,'Pr(>|z|)']
+ return(dum)
+ }
The eval_model_nonimpvar function with using cv_nonimpvar function calculates and plots the boxplot of p-values of coefficients through a repeated (100 times) 10-fold cross-validation for the given formula fml of the model.
R> cv_nonimpvar <- function(fml, folds)
+ {
+ rs <- lapply(folds, function(x)
+ {
+ train_set_train <- train_set[-x, ]
+ mdl <- glm(formula = fml, family = binomial(link=logit), data = train_set_train)
+ nonimpvar <- pvalue.coef(mdl)
+ return(nonimpvar)
+ })
+ vars_name <- all.vars(fml[[3]])
+ rs_matrix <- matrix(unlist(rs), nrow=length(vars_name)+1 )
+ colnames(rs_matrix) <- c(paste0('Fold0',1:9),'Fold10')
+ rownames(rs_matrix) <- c('Intercept', vars_name)
+ return(rs_matrix)
+ }
R> n.cv <- 100
R> eval_model_nonimpvar <- function(fml)
+ {
+ t.mat <- NULL
+ for (i in 1:n.cv)
+ {
+ folds.new <- createFolds(train_set$default, k = 10)
+ cv_var_op <- cv_nonimpvar(fml, folds.new)
+ t.mat <- cbind(t.mat, cv_var_op)
+ }
+ dum <- apply(t.mat, 1, mean)
+ id <- order(dum, decreasing = T)
+ boxplot(t(t.mat[id,]), las=2, main=fml, ylim=c(0,.2))
+ points(dum[id], pch=20, cex=1, col='red')
+ return(t.mat)
+}
Applying for the most general model:
fml0 <- default ~ V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12+V13+V14+V15+V16+V17+V18+V19+V20+V21+V22+V23+V24 nonimpvar0.mat <- eval_model_nonimpvar(fml0)
I obtain the below results:
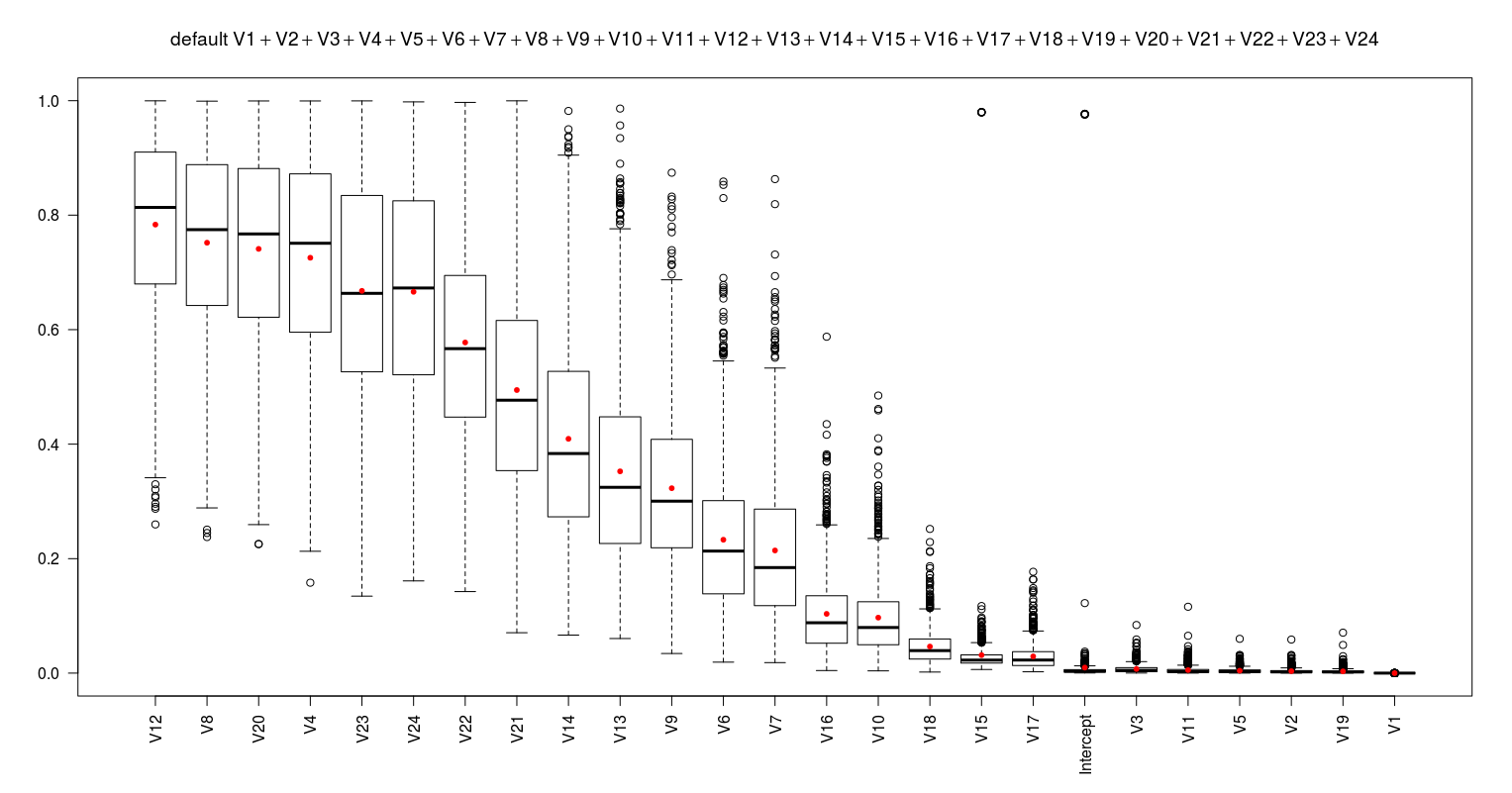
These results suggest to remove the V12 to form a better model (fml1). After removing it I repeat the same procedure to obtain the next worst predictor. I continue this procedure till all the predictors show the average p-value less than 0.05. This proposes 16 models (as below) which are simpler than the fml0.
#-------------------------------------------------------------------------------------------------------- fml1 <- default ~ V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V13+V14+V15+V16+V17+V18+V19+V20+V21+V22+V23+V24 #12 nonimpvar1.mat <- eval_model_nonimpvar(fml1) #-------------------------------------------------------------------------------------------------------- fml2 <- default ~ V1+V2+V3+V4+V5+V6+V7+V9+V10+V11+V13+V14+V15+V16+V17+V18+V19+V20+V21+V22+V23+V24 #12, 8 nonimpvar2.mat <- eval_model_nonimpvar(fml2) #-------------------------------------------------------------------------------------------------------- fml3 <- default ~ V1+V2+V3+V4+V5+V6+V7+V9+V10+V11+V13+V14+V15+V16+V17+V18+V19+V21+V22+V23+V24 #12, 8, 20 nonimpvar3.mat <- eval_model_nonimpvar(fml3) #-------------------------------------------------------------------------------------------------------- fml4 <- default ~ V1+V2+V3+V5+V6+V7+V9+V10+V11+V13+V14+V15+V16+V17+V18+V19+V21+V22+V23+V24 #12, 8, 20, 4 nonimpvar4.mat <- eval_model_nonimpvar(fml4) #-------------------------------------------------------------------------------------------------------- fml5 <- default ~ V1+V2+V3+V5+V6+V7+V9+V10+V11+V13+V14+V15+V16+V17+V18+V19+V21+V22+V24 #12, 8, 20, 4, 23 nonimpvar5.mat <- eval_model_nonimpvar(fml5) #-------------------------------------------------------------------------------------------------------- fml6 <- default ~ V1+V2+V3+V5+V6+V7+V9+V10+V11+V13+V14+V15+V16+V17+V18+V19+V21+V22 #12, 8, 20, 4, 23, 24 nonimpvar6.mat <- eval_model_nonimpvar(fml6) #-------------------------------------------------------------------------------------------------------- fml7 <- default ~ V1+V2+V3+V5+V6+V7+V9+V10+V11+V13+V14+V15+V16+V17+V18+V19+V21 #12, 8, 20, 4, 23, 24, 22 nonimpvar7.mat <- eval_model_nonimpvar(fml7) #-------------------------------------------------------------------------------------------------------- fml8 <- default ~ V1+V2+V3+V5+V6+V7+V9+V10+V11+V13+V15+V16+V17+V18+V19+V21 #12, 8, 20, 4, 23, 24, 22, 14 nonimpvar8.mat <- eval_model_nonimpvar(fml8) #-------------------------------------------------------------------------------------------------------- fml9 <- default ~ V1+V2+V3+V5+V6+V7+V9+V10+V11+V13+V15+V16+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21 nonimpvar9.mat <- eval_model_nonimpvar(fml9) #-------------------------------------------------------------------------------------------------------- fml10 <- default ~ V1+V2+V3+V5+V6+V7+V9+V10+V11+V15+V16+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21, 13 nonimpvar10.mat <- eval_model_nonimpvar(fml10) #-------------------------------------------------------------------------------------------------------- fml11 <- default ~ V1+V2+V3+V5+V7+V9+V10+V11+V15+V16+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21, 13, 6 nonimpvar11.mat <- eval_model_nonimpvar(fml11) #-------------------------------------------------------------------------------------------------------- fml12 <- default ~ V1+V2+V3+V5+V9+V10+V11+V15+V16+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21, 13, 6, 7 nonimpvar12.mat <- eval_model_nonimpvar(fml12) #-------------------------------------------------------------------------------------------------------- fml13 <- default ~ V1+V2+V3+V5+V10+V11+V15+V16+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21, 13, 6, 7, 9 nonimpvar13.mat <- eval_model_nonimpvar(fml13) #-------------------------------------------------------------------------------------------------------- fml14 <- default ~ V1+V2+V3+V5+V11+V15+V16+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21, 13, 6, 7, 9, 10 nonimpvar14.mat <- eval_model_nonimpvar(fml14) #-------------------------------------------------------------------------------------------------------- fml15 <- default ~ V1+V2+V3+V5+V11+V15+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21, 13, 6, 7, 9, 10, 16 nonimpvar15.mat <- eval_model_nonimpvar(fml15) #-------------------------------------------------------------------------------------------------------- fml16 <- default ~ V1+V2+V3+V5+V11+V17+V18+V19 #12, 8, 20, 4, 23, 24, 22, 14, 21, 13, 6, 7, 9, 10, 16, 15 nonimpvar16.mat <- eval_model_nonimpvar(fml16) #--------------------------------------------------------------------------------------------------------
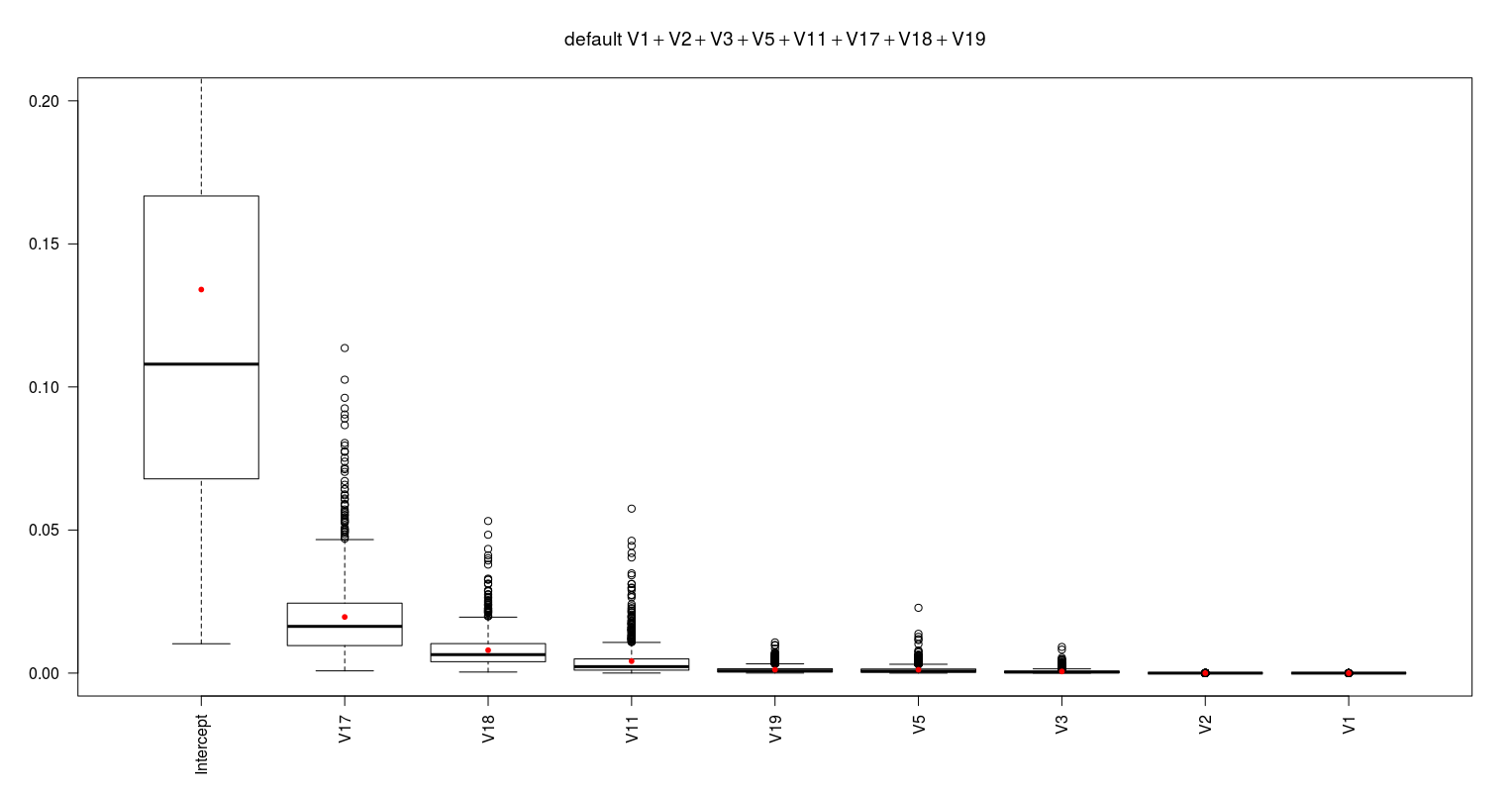
The following figure shows the p-values of the coefficient of the last model (fml16).
Having 17 models I evaluate them based on AUC (Area Under ROC). I use pROC and caret packages to calculate average AUC for models using repeated (100 times) 10-fold cross-validation.
library(pROC)
cv_auc_function <- function(fml, folds)
{
auc_r <- lapply(folds, function(x)
{
train_set_train <- train_set[-x, ]
train_set_test <- train_set[x, ]
mdl <- glm(formula = fml, family = binomial(link=logit), data = train_set_train)
pred <- predict(mdl, newdata = train_set_test, type = 'response')
dum.roc <- roc(train_set_test$default, pred)
as.vector(auc(dum.roc))
})
return(unlist(auc_r))
# Output is a vector like:
# Fold01 Fold02 Fold03 Fold04 Fold05 Fold06 Fold07 Fold08 Fold09 Fold10
# 0.7456522 0.8832952 0.8478261 0.8836957 0.7652174 0.6904255 0.7425532 0.7356979 0.7804348 0.7739130
}
#.............................................
fml_vec <- paste0('fml', 0:16)
auc_matrix_cv <- NULL
for (i in fml_vec)
{
fml <- get(i)
t.vec <- NULL
for ( j in 1:n.cv)
{
folds.new <- createFolds(train_set$default, k = 10)
dum <- cv_auc_function(fml, folds.new)
t.vec <- c(t.vec, dum)
}
auc_matrix_cv <- cbind(auc_matrix_cv, t.vec)
}
colnames(auc_matrix_cv) <- fml_vec
auc_means <- apply(auc_matrix_cv, 2, mean)
id <- order(auc_means, decreasing = T)
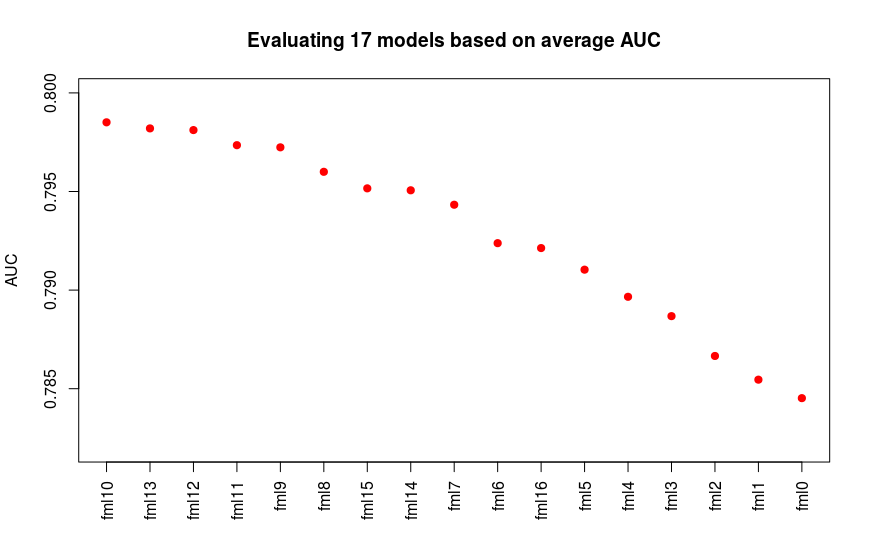
plot(auc_means[id], xaxt='n', xlab='', ylim=c(0.782, 0.8), pch=20,cex=1.5, col='red', ylab='AUC', main='Evaluating all 16 models based on AUC via CV') #CV2.png
axis(1,at=1:17,labels=names(auc_means[id]), las=2)
As we see in the results in following plot the fml10 shows the best average AUC while followed by fml13, fml12 and fml11 models.
For a bank apart from a demand for high accuracy, sensitivity and specificity of a model, a low value of the bad rate is also desired. The bad rate is defined as the ratio of false negative to the total actual negative examples. The low value of bad rate shows the less number of actual positive default cases which are wrongly predicted as the non-default cases. This reduces the risk of loss for the bank. Although a low bad rate is desirable but it must along with a proper percentage of acceptance ratio of applicants. For this project I assume a maximum of 15% bad rate and minimum 60% acceptance ratio are reasonable for a particular bank. Therefore I try to find the best model which can satisfy these criteria.
The following br.se.ac function calculate the bad rate, sensitivity, specificity, accuracy and kappa statistics in the range of 0% to 100% acceptance ratio for a particular model.
#------br.se.ac function--------------------------------------------------
br.se.ac <- function(actl_class, pred_prob)
{
acp_rate <- seq(0,1,by=0.01)
cut_off <- NULL
bad_rate <- NULL
sens <- NULL
spec <- NULL
accu <- NULL
kppa <- NULL
for (i in 1:length(acp_rate))
{
cutoff <- quantile(pred_prob, acp_rate[i])
pred_class <- ifelse(pred_prob> cutoff, 1, 0)
pred_class <- factor(pred_class, levels=levels(actl_class))
cont_table <- table(actl_class, pred_class)
TN <- cont_table[1,1]
FP <- cont_table[1,2]
FN <- cont_table[2,1]
TP <- cont_table[2,2]
br <- FN/(FN+TN)
se <- TP/(TP+FN)
sp <- TN/(TN+FP)
ac <- (TN+TP)/(TN+FP+FN+TP)
py <- ((TP+FN)/(TN+FP+FN+TP)) * ((TP+FP)/(TN+FP+FN+TP))
pn <- ((FP+TN)/(TN+FP+FN+TP)) * ((FN+TN)/(TN+FP+FN+TP))
pe <- py+pn
kp <- (ac-pe)/(1-pe)
cut_off <- c(cut_off, cutoff)
bad_rate <- c(bad_rate, br)
sens <- c(sens, se)
spec <- c(spec, sp)
accu <- c(accu, ac)
kppa <- c(kppa, kp)
}
data.frame(acp_rate, cut_off, bad_rate, sens, spec, accu, kppa)
}
The below function and codes calculate and plot the average bad rate vs acceptance ratio for all suggested model through repeated (100 times) 10-fold cross-validation.
cv_br_function <- function(fml, folds)
{
br_r <- lapply(folds, function(x)
{
train_set_train <- train_set[-x, ]
train_set_test <- train_set[x, ]
mdl <- glm(formula = fml, family = binomial(link=logit), data = train_set_train)
pred <- predict(mdl, newdata = train_set_test, type = 'response')
dum <- br.se.ac(train_set_test$default, pred )
return(dum$bad_rate)
})
br.matrix <- matrix(unlist(br_r), ncol=10 )
colnames(br.matrix) <- c(paste0('Fold0',1:9),'Fold10')
rownames(br.matrix) <- paste0(0:100,'%')
return(br.matrix)
}
#....Calculating average bad rate for each model via CV...........
for (i in fml_vec)
{
print(i)
t.mat <- NULL
for ( j in 1:n.cv)
{
folds.new <- createFolds(train_set$default, k = 10)
dum <- cv_br_function(get(i), folds.new)
t.mat <- cbind(t.mat, dum)
}
dum2 <- apply(t.mat, 1, mean)
dum3 <- paste0(i,'_br.cv')
assign(dum3, dum2)
}
#..................plotting...................
#for (j in fml_vec)
#{
plot(seq(0,1,by=0.01), rep(0, 101), type='n', ylim=c(0,0.3), xlab='Acceptance Rate', ylab='Bad Rate', main='Average bad rate based on CV')
for (i in fml_vec)
{
fml <- get(i)
dum3 <- paste0(i,'_br.cv') # "fml20_br.cv"
lines(seq(0,1,by=0.01), get(dum3), type='o', col='grey', pch=20)
}
col_vec <- c('blue', 'black', 'darkgreen', 'red', 'orange','brown', 'skyblue', 'red')
cnt <- 0
for (i in c('fml10', 'fml13', 'fml12', 'fml11', 'fml0'))
{
cnt <- cnt+1
dum3 <- paste0(i,'_br.cv')
lines(seq(0,1,by=0.01), get(dum3), type='o', col=col_vec[cnt], pch=20) # CV3.png
}
abline(h=0.1, lty=2)
abline(h=0.15, lty=2)
text(0.05, 0.3, 'fml10', cex=1.3)
text(0.05, 0.29, 'fml13', cex=1.3)
text(0.05, 0.28, 'fml12', cex=1.3)
text(0.05, 0.27, 'fml11', cex=1.3)
text(0.05, 0.26, 'fml0', cex=1.3)
points(0.02, 0.3, pch=20, cex=1.3, col='blue')
points(0.02, 0.29, pch=20, cex=1.3, col='black')
points(0.02, 0.28, pch=20, cex=1.3, col='darkgreen')
points(0.02, 0.27, pch=20, cex=1.3, col='red')
points(0.02, 0.26, pch=20, cex=1.3, col='orange')
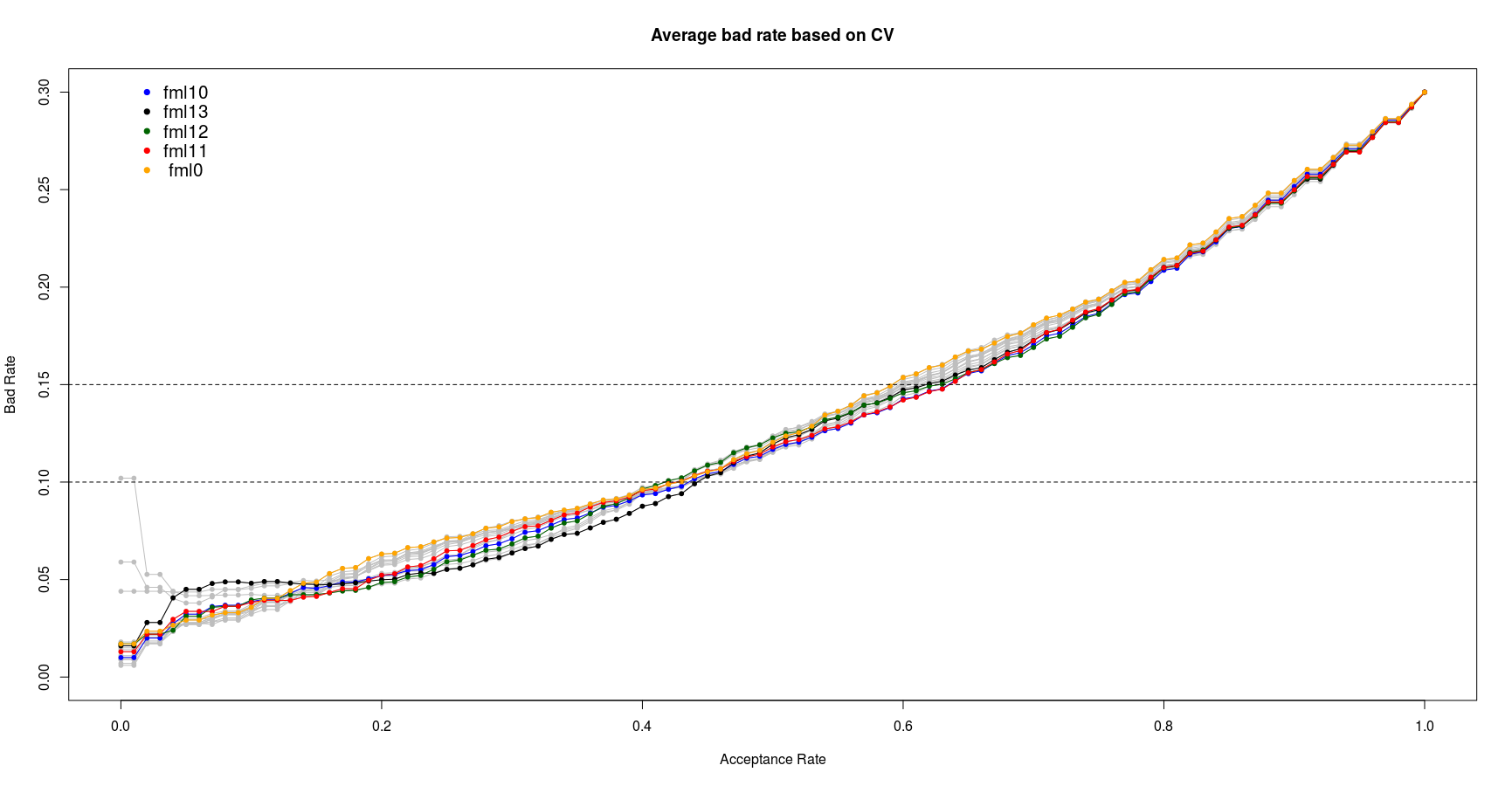
From the above plot we can see the fml10 and fml11 show the best performance in bad rate between 10% to 15%. Since the fml10 has already shown the better AUC I select the fml10 as the best logistic model. It worth note that this model is selected based on the training data set. Its actual performance will be checked in the last section of this report on unseen test data set.
2- Decision Tree
Similar to logistic regression first I split the data to training and test sets.
R> in_train <- createDataPartition(d.g$default, p = 0.66, list = FALSE) R> train_set <- d.g[in_train,] R> test_set <- d.g[-in_train,] R> prop.table(table(train_set$default)) Nondef Def 0.7 0.3 R> prop.table(table(test_set$default)) Nondef Def 0.7 0.3
I use rpart & rpart.plot packages for applying decision tree algorithm and plotting trees. First I construct the trees with different complexity parameter values and choose the proposed trees based on the minimum average cross-validate error.
R> library(rpart)
R> library(rpart.plot)
R> xerr.matrix <- NULL
R> for ( i in 1:1000)
+ {
+ fml1 <- rpart(default ~ ., method = "class", data = train_set, control = rpart.control(cp = 0.0001))
+ dum <- printcp(fml0)
+ xerr.matrix <- cbind(xerr.matrix, dum[,4])
+ }
R> rownames(xerr.matrix) <- round(dum[,1], digits=6)
R> boxplot(t(xerr.matrix))
R> mean.xerr <- apply(xerr.matrix, 1, mean)
R> points(1:7, mean.xerr, pch=20, col='red', cex=2)
The results are plotted below:
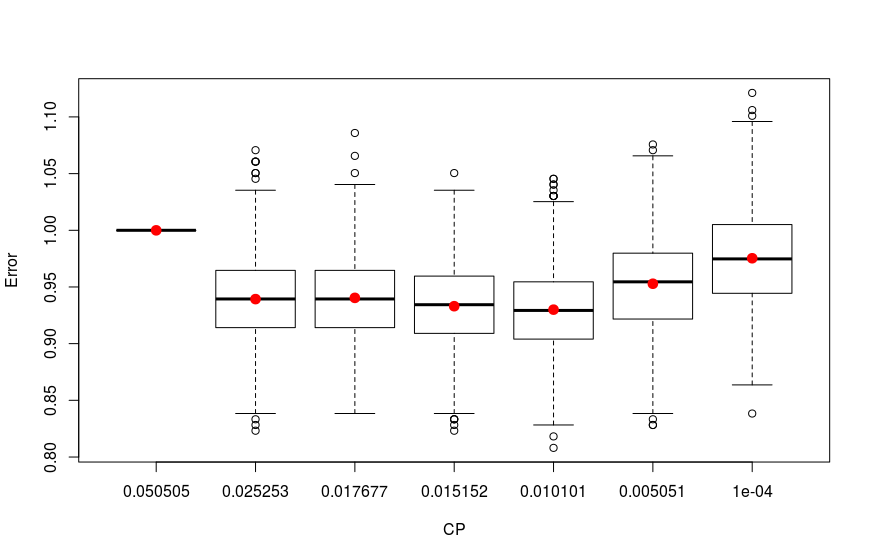
As we see the four trees with 0.01010101, 0.01515152, 0.01767677 and 0.02525253 CP values have the lowest errors. To have a view on this tree I construct and prune trees with these CP values and plot them:
R> id <- which.min(mean.xerr) R> cp.best.xrr <- dum[id,1] #[1] 0.01010101 R> cp.table.sample <- dum R> fml2 <- prune(fml0, cp = cp.best.xrr) # 0.01010101 R> fml3 <- prune(fml0, cp = dum[4,1]) # 0.01515152 R> fml4 <- prune(fml0, cp = dum[3,1]) # 0.01767677 R> fml5 <- prune(fml0, cp = dum[2,1]) # 0.02525253
The prp function is used to plot trees:
R> for (i in paste0('fml', 1:5))
+ {
+ png(file=paste0(i,'.png'), width = 1500, height = 800)
+ prp(get(i), main=i)
+ dev.off()
+ }
In the below figures you can see and compare the fml1 and fml5:
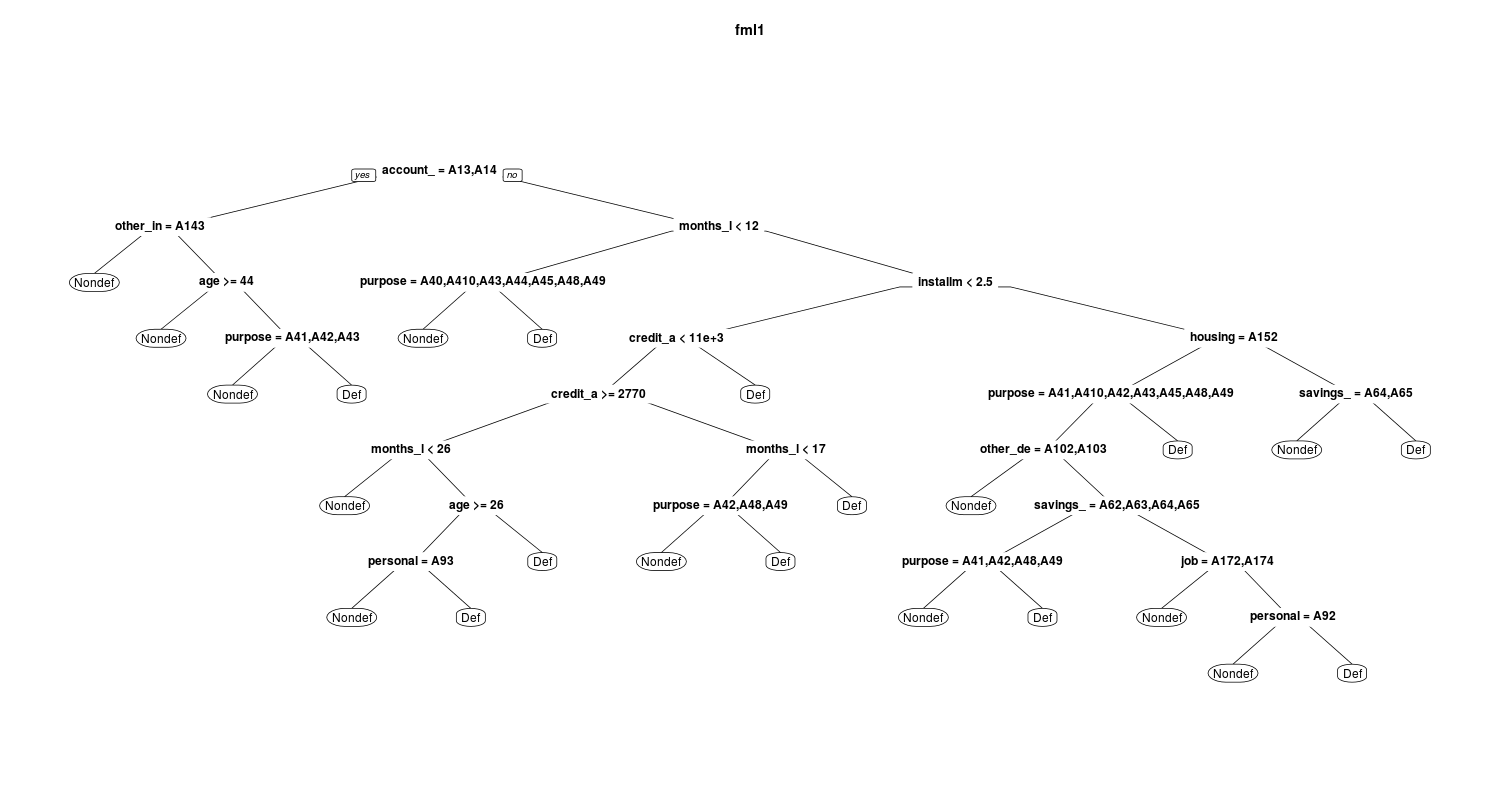
and
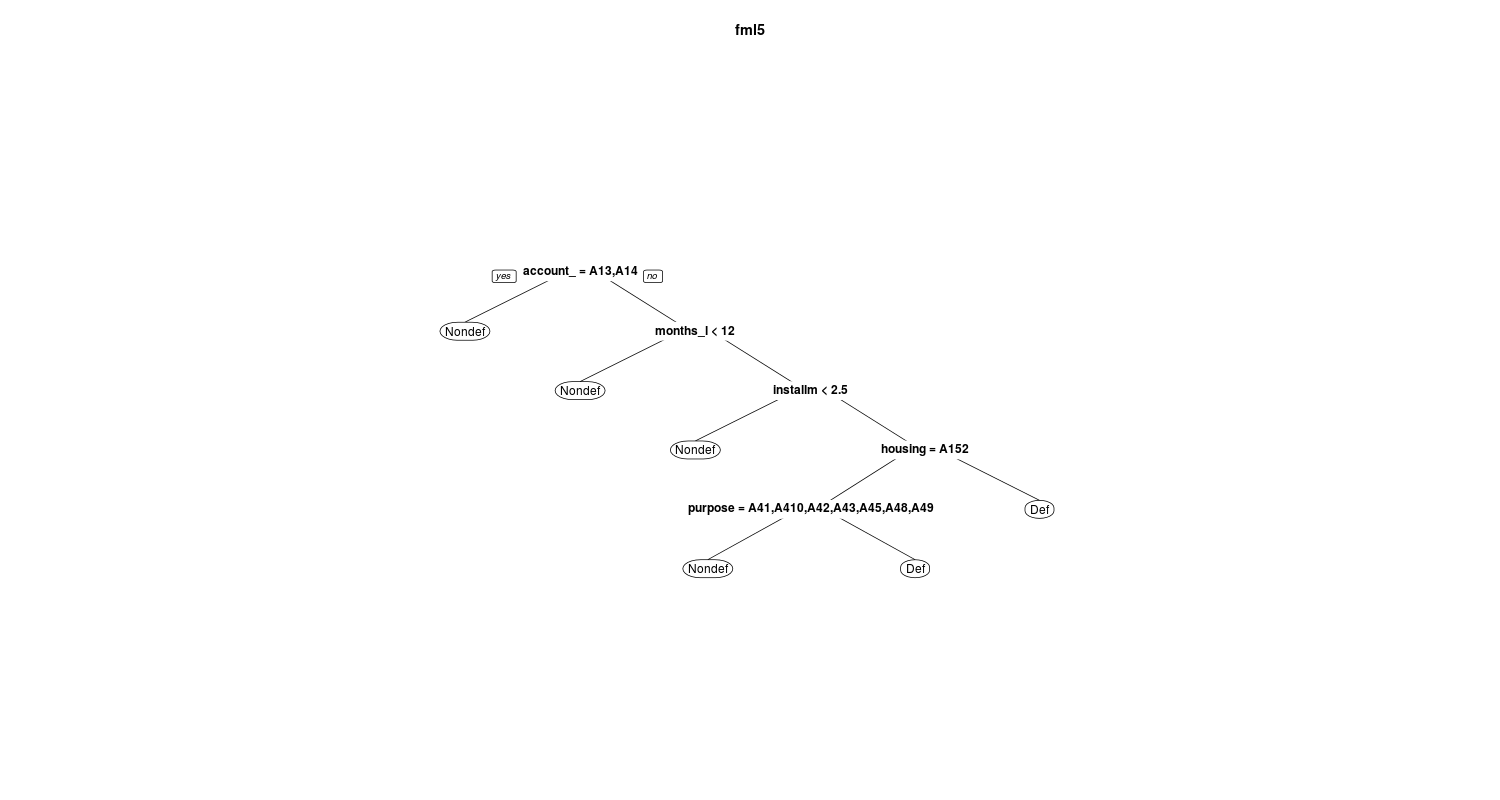
I also select the trees based on the average AUC value using train function in caret package. To speed up the computation I construct a parallel backend using doMC package:
R> library(doMC)
R> registerDoMC(cores = 9)
R> tc <- trainControl(method = "repeatedcv", number = 10, repeats = 100, classProbs = TRUE, summaryFunction=twoClassSummary)
R> rpart.grid <- expand.grid(.cp=c(1e-7,0.0001,0.0004, 0.0005, seq(0.001, 0.03, by=0.001), seq(0.04,0.06, by=0.005)) )
R> train.rpart.rcv <- train(default ~ .,
data=train_set, method="rpart",
trControl=tc, tuneGrid=rpart.grid, metric='ROC')
R> registerDoSEQ()
The below figure shows the result:
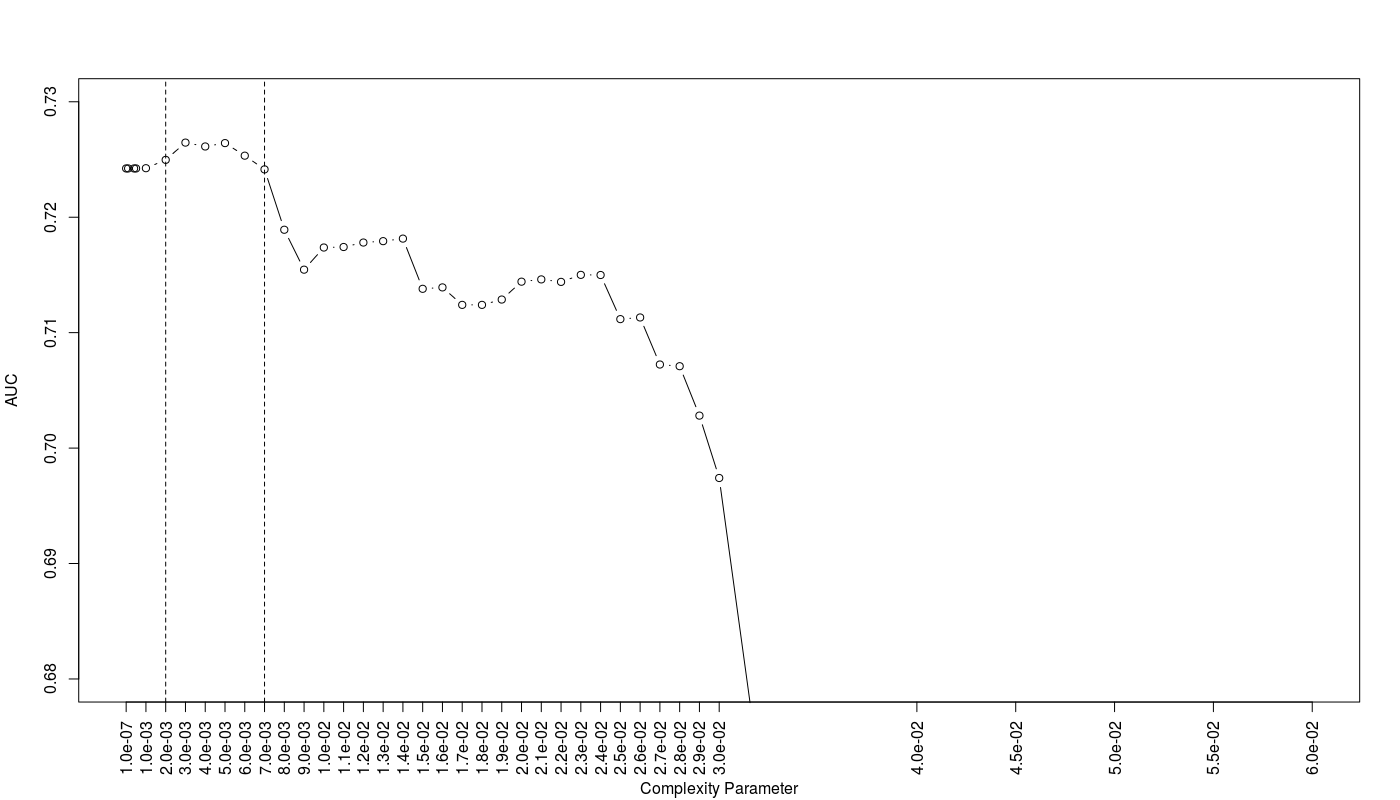
As we can see the trees with CP values between 0.002 to 0.007 show the best AUC efficiency. Totally I have 10 proposed trees with different CP values.
Following the similar procedure in evaluation of logistic models, I evaluate 10 proposed trees based on their bad rate and other statistics through below codes and functions:
#------br.se.ac function--------------------------------------------------
R> br.se.ac <- function(actl_class, pred_prob)
+ {
+ acp_rate <- seq(0,1,by=0.01)
+ cut_off <- NULL
+ bad_rate <- NULL
+ sens <- NULL
+ spec <- NULL
+ accu <- NULL
+ kppa <- NULL
+ for (i in 1:length(acp_rate))
+ {
+ cutoff <- quantile(pred_prob, acp_rate[i])
+ pred_class <- ifelse(pred_prob> cutoff, 'Def', 'Nondef')
+ pred_class <- factor(pred_class, levels=levels(actl_class))
+ cont_table <- table(actl_class, pred_class)
+ TN <- cont_table[1,1]
+ FP <- cont_table[1,2]
+ FN <- cont_table[2,1]
+ TP <- cont_table[2,2]
+ br <- FN/(FN+TN)
+ se <- TP/(TP+FN)
+ sp <- TN/(TN+FP)
+ ac <- (TN+TP)/(TN+FP+FN+TP)
+ py <- ((TP+FN)/(TN+FP+FN+TP)) * ((TP+FP)/(TN+FP+FN+TP))
+ pn <- ((FP+TN)/(TN+FP+FN+TP)) * ((FN+TN)/(TN+FP+FN+TP))
+ pe <- py+pn
+ kp <- (ac-pe)/(1-pe)
+ cut_off <- c(cut_off, cutoff)
+ bad_rate <- c(bad_rate, br)
+ sens <- c(sens, se)
+ spec <- c(spec, sp)
+ accu <- c(accu, ac)
+ kppa <- c(kppa, kp)
+ }
+ data.frame(acp_rate, cut_off, bad_rate, sens, spec, accu, kppa)
+ }
#----cv_br_function ------------------------------------------------------------
R> cv_br_function <- function(cp_par, folds)
+ {
+ br_r <- lapply(folds, function(x)
+ {
+ train_set_train <- train_set[-x, ]
+ train_set_test <- train_set[x, ]
+ mdl <- rpart(default ~ ., method = "class", data = train_set_train, control = rpart.control(cp = cp_par))
+ pred <- predict(mdl, newdata = train_set_test, type='prob')
+ dum <- br.se.ac(train_set_test$default, pred[,2] )
+ return(dum$bad_rate)
+ })
+ br.matrix <- matrix(unlist(br_r), ncol=10 )
+ colnames(br.matrix) <- c(paste0('Fold0',1:9),'Fold10')
+ rownames(br.matrix) <- paste0(0:100,'%')
+ return(br.matrix)
+ }
#....Calculating average bad rate for each tree via repeated CV...........
R> n.cv <- 100
R> cp_vec <- c( seq(0.002, 0.007, by=0.001), 0.01010101, 0.01515152, 0.01767677, 0.02525253)
R> for (cp_p in cp_vec)
+ {
+ print(cp_p)
+ t.mat <- NULL
+ for ( j in 1:n.cv)
+ {
+ folds.new <- createFolds(train_set$default, k = 10)
+ dum <- cv_br_function(cp_p, folds.new)
+ t.mat <- cbind(t.mat, dum)
+ }
+ dum2 <- apply(t.mat, 1, mean)
+ dum3 <- paste0('fml_cp_',cp_p,'_br.cv') # e.g. "fml_cp_0.002_br.cv"
+ assign(dum3, dum2)
+ }
#..................plotting...................
plot(seq(0,1,by=0.01), rep(0, 101), type='n', ylim=c(0,0.3), xlab='Acceptance Rate', ylab='Bad Rate', main='Average bad rate based on CV')
for (cp_p in cp_vec)
{
dum3 <- paste0('fml_cp_',cp_p,'_br.cv') # "fml_cp_0.002_br.cv"
lines(seq(0,1,by=0.01), get(dum3), type='o', col='grey', pch=20)
}
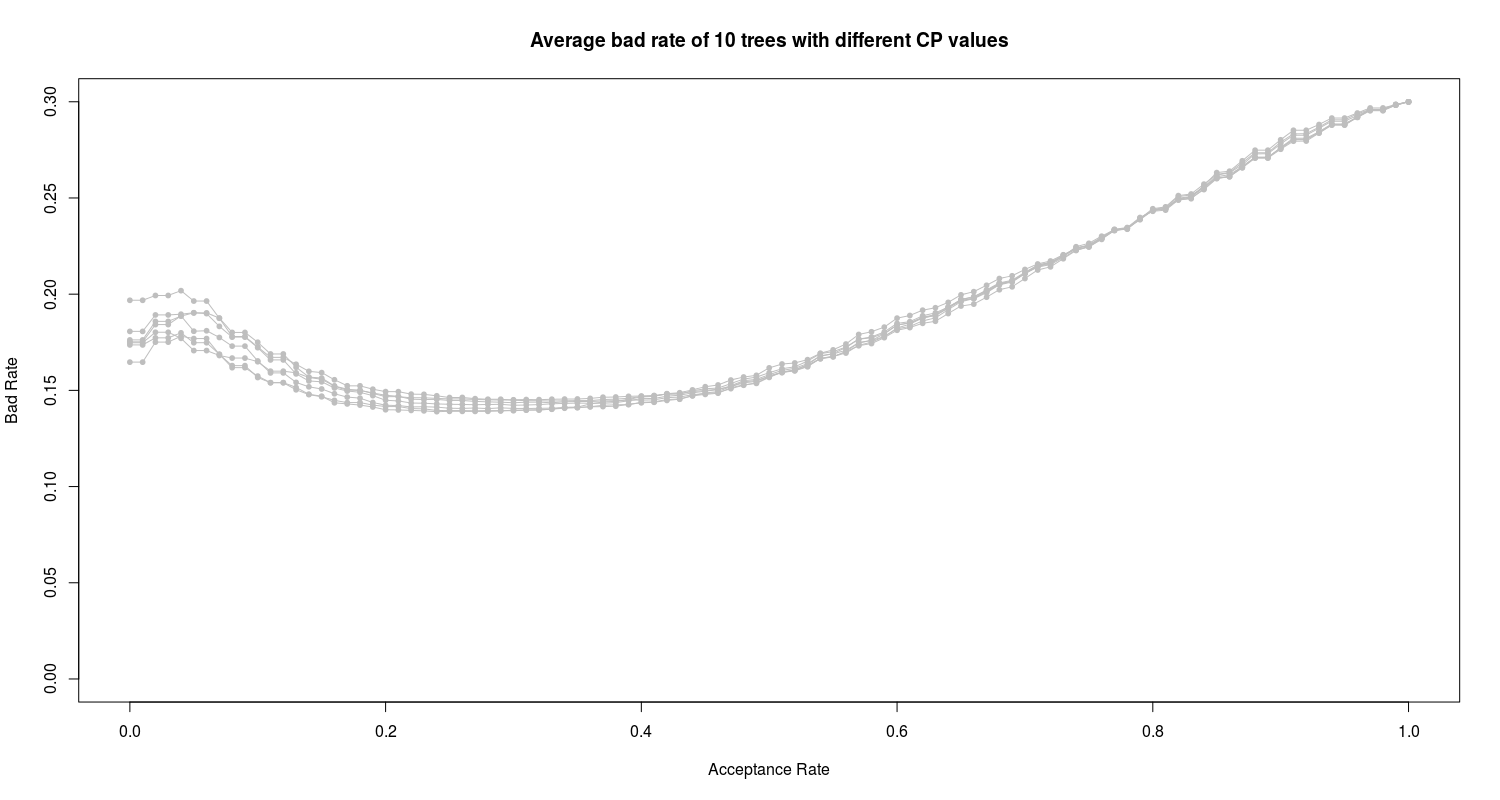
We can see the high bad rate of all 10 proposed trees. In the next section I employ and train the random forest algorithm on the data.
3. Random Forest
Using caret package I train random forest on training data set considering AUC for different mtry values (number of features which are randomly selected at each split) in a repeated cross-validation method. I also use a parallel backend to speed up the computation.
library(caret) library(doMC) registerDoMC(cores = 12) tc <- trainControl(method = "repeatedcv", number = 10, repeats = 100, classProbs = TRUE, summaryFunction=twoClassSummary) rf_grid <- expand.grid(.mtry = c(2, 3, 4, 5, 6, 7, 8, 9, 10, 16, 20)) m_rf <- train(default ~ ., data = train_set, method = "rf", metric = "ROC", trControl = tc, tuneGrid = rf_grid) registerDoSEQ()
I plot the results as below:
plot(m_rf$results$mtry, m_rf$results$ROC, typ='b', xaxt='n', xlab='mtry', ylab='AUC') axis(1,at= c(2, 3, 4, 5, 6, 7, 8, 9, 10, 16, 20) , las=2,col.axis='black',col='black')
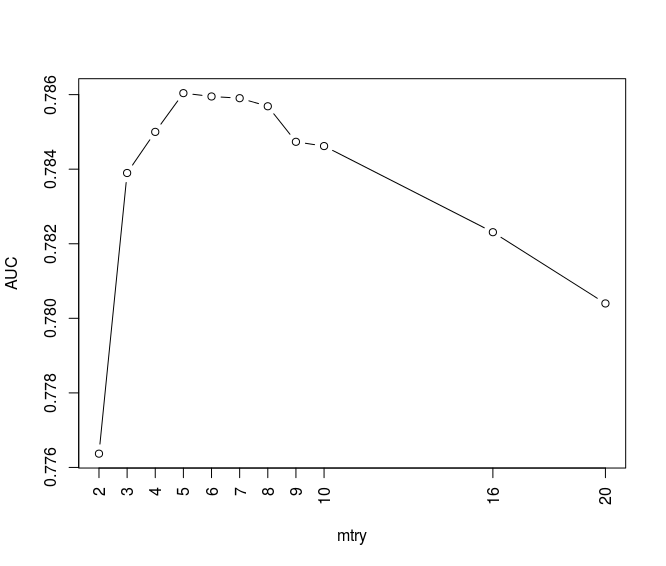
We can see the random forest corresponding to mtry values between 3 to 10 shows high values in AUC. Using br.se.ac function in previous section and below codes and functions I calculate the bad rate all proposed random forest models:
#----Evaluating and plotting of bad rate vs acceptance rate of all *RANDOM FOREST* models bulit on CV---------------------------------------------------
R> cv_br_function_rf <- function(mtry_par, folds)
+ {
+ br_r <- lapply(folds, function(x)
+ {
+ train_set_train <- train_set[-x, ]
+ train_set_test <- train_set[x, ]
+ mdl <- randomForest(default ~ ., data = train_set_train, ntree=500, mtry=mtry_par)
+ pred <- predict(mdl, newdata=train_set_test, type = 'prob')
+ dum <- br.se.ac(train_set_test$default, pred[,2] )
+ return(dum$bad_rate)
+ })
+ br.matrix <- matrix(unlist(br_r), ncol=10 )
+ colnames(br.matrix) <- c(paste0('Fold0',1:9),'Fold10')
+ rownames(br.matrix) <- paste0(0:100,'%')
+ return(br.matrix)
+}
#....Calculating average bad rate for each model via CV...........
R> library(randomForest)
R> n.cv <- 100
R> mtry_vec <- 3:10
R> for (mtry_p in mtry_vec)
+ {
+ t.mat <- NULL
+ for ( j in 1:n.cv)
+ {
+ folds.new <- createFolds(train_set$default, k = 10)
+ dum <- cv_br_function_rf(mtry_p, folds.new)
+ t.mat <- cbind(t.mat, dum)
+ }
+ dum2 <- apply(t.mat, 1, mean)
+ dum3 <- paste0('fml_mtry_',mtry_p,'_br.cv') # e.g. "fml_mtry_3_br.cv"
+ assign(dum3, dum2)
+ }
The results are plotted:
R> plot(seq(0,1,by=0.01), rep(0, 101), type='n', ylim=c(0,0.3), xlab='Acceptance Rate', ylab='Bad Rate', main='Average bad rate of 10 trees (gold color) and 8 random forest models (grey)')
R> for (cp_p in cp_vec)
+ {
+ dum3 <- paste0('fml_cp_',cp_p,'_br.cv') # e.g. "fml_cp_0.002_br.cv"
+ lines(seq(0,1,by=0.01), get(dum3), type='o', col='lightgoldenrod', pch=20)
+ }
R> for (mtry_p in mtry_vec)
+ {
+ dum3 <- paste0('fml_mtry_',mtry_p,'_br.cv') # e.g. "fml_mtry_10_br.cv"
+ lines(seq(0,1,by=0.01), get(dum3), type='o', col='grey', pch=20)
+ }
R> lines(seq(0,1,by=0.01), fml_mtry_3_br.cv, type='o', col='red', pch=20)
R> abline(h=0.1, lty=2)
R> abline(h=0.15, lty=2)
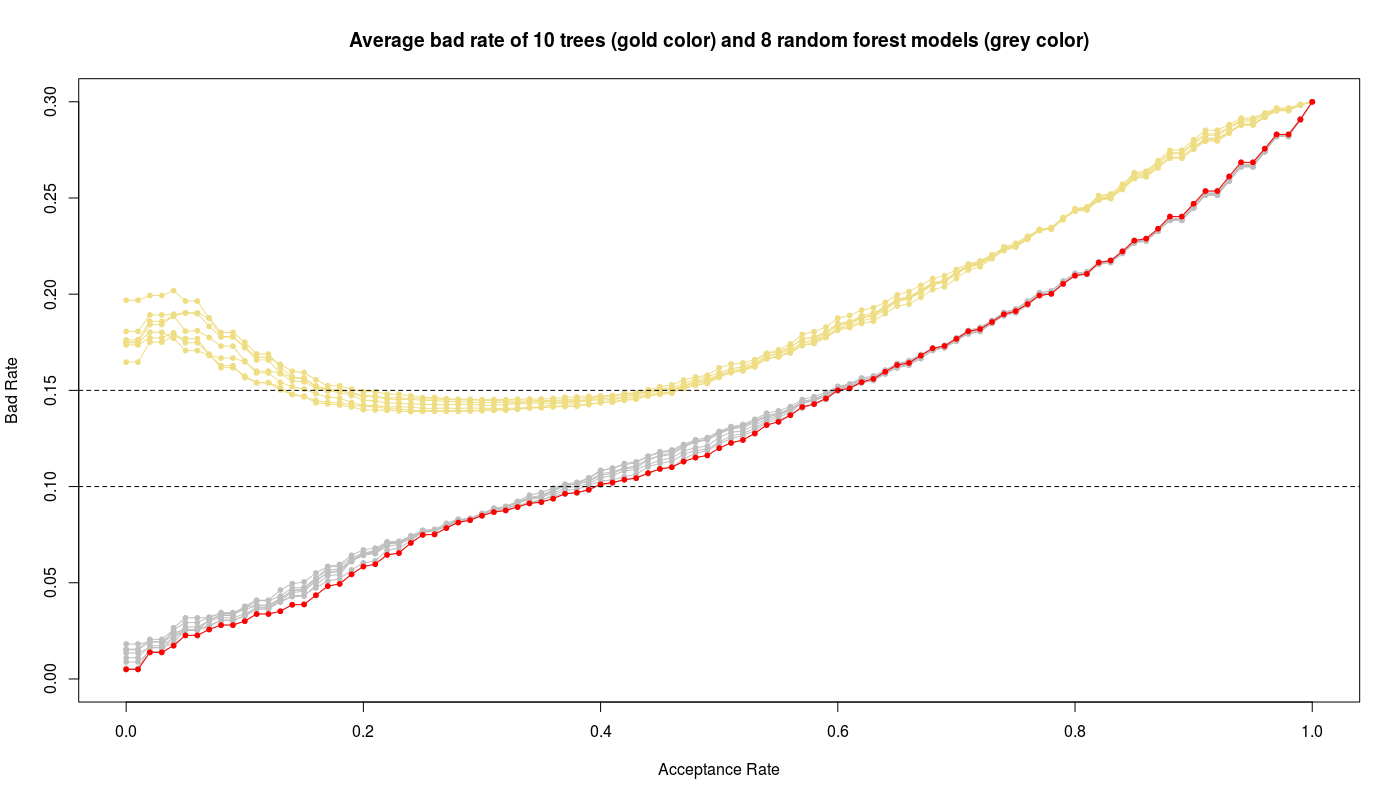
In above figure I have also plotted the results of trees (gold color) to compare with random forest models (gray color). We see obviously the random forest models work better than trees while the random forest with mtry=3 gives the best performance i.e. low bad rate and high acceptance rate.
Results of the final models
The fml10 logistic model and random forest with mtry=3 are the winners on training data set. To see the real performance of both models I test them on unseen test data set. The logistic fml10 model can evaluate via using br.se.ac function defined in logistic section as:
mdl <- glm(formula = fml10, family = binomial(link=logit), data = train_set) pred <- predict(mdl, newdata = test_set, type = 'response') log_fml10_results <- br.se.ac(test_set$default, pred )
Since random forest has the randomness inherent I calculate a average of performance of the model with mtry=3:
R> sum_mat <- matrix(0, nrow=101,ncol=7)
R> for (i in 1:100)
+ {
+ mdl <- randomForest(default ~ ., data = train_set, ntree=500, mtry=3)
+ pred <- predict(mdl, newdata=test_set, type = 'prob')
+ dum <- br.se.ac(test_set$default, pred[,2] )
+ sum_mat <- sum_mat + dum
+ }
R> rf_mtry3_results <- sum_mat/100
Assuming maximum 15% bad rate we have:
acp_rate cut_off bad_rate sens spec accu kppa Logistic Regression 65% 0.65 0.44823798 0.14932127 0.67647059 0.789915966 0.7558824 0.445187166 Random Forest 63% 0.63 0.4042546 0.151472427 0.68137255 0.764957983 0.7398824 0.418835806
The below figure illustrates the bad rate for both models:
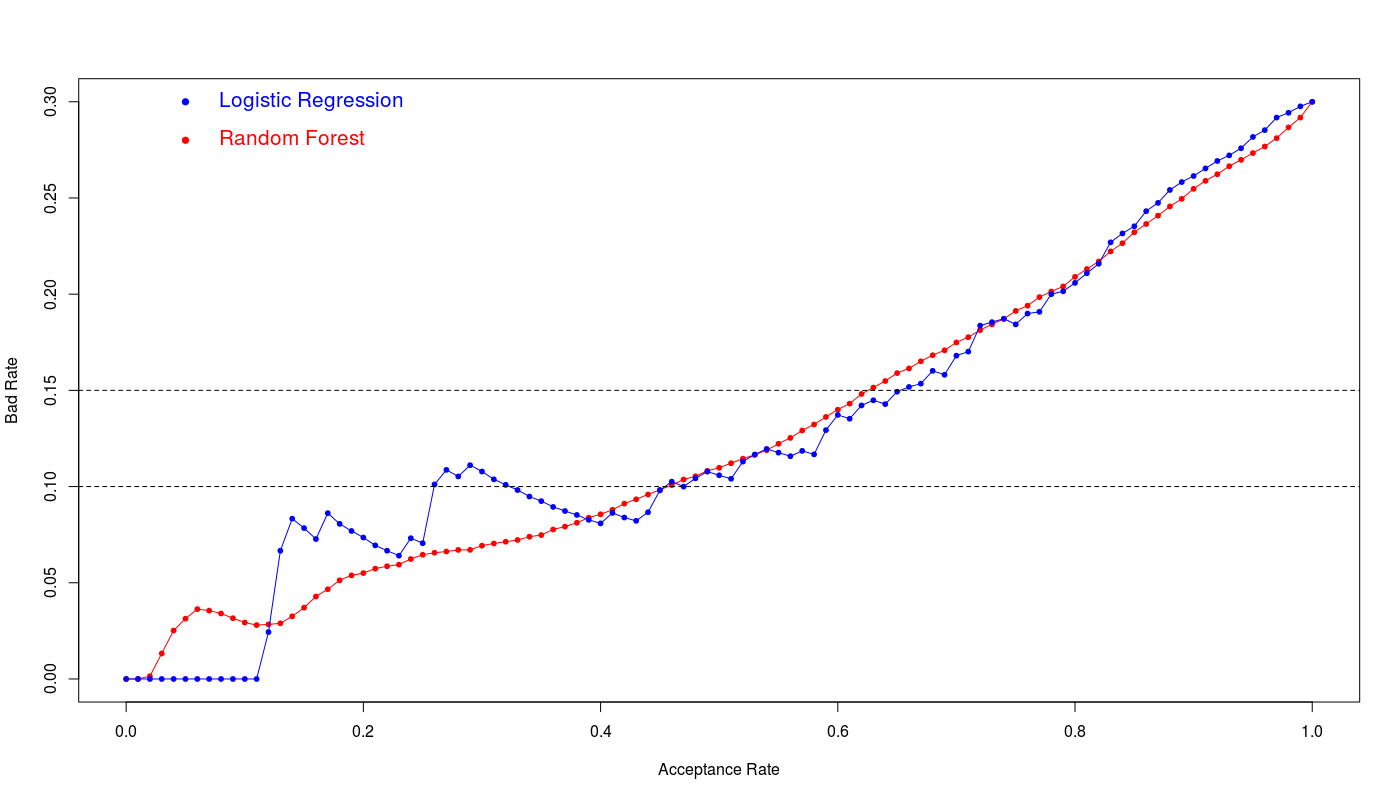
We see the logistic regression and random forest show the similar efficiency however logistic regression shows slightly better performance at 15% bad rate. The 65% acceptance ratio at 15% bad rate with 76% accuracy and 0.44 kappa value is a good achievement for this model.